1-.
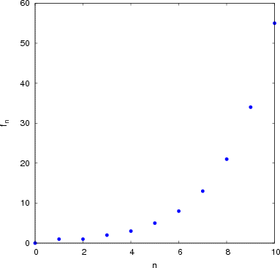
Y qué mejor forma de empezar que planteándonos un problema que se planteó Leonardo de Pisa, más conocido como FIBONACCI allá por el año 1202: En un recinto cerrado tenemos una pareja de conejos (macho y hembra) de un mes de edad que aún no pueden reproducirse, pero que podrán hacerlo al segundo mes de edad. Supongamos que la gestación es de un mes, y que cada mes, a partir del segundo, cada pareja siempre dará origen a otra nueva pareja (macho y hembra también). Si cada pareja de conejos se reproduce de la misma forma que la pareja inicial, y si suponemos que no se mueren, ¿cuántas parejas habrá en cada mes? Piénsalo e intenta averiguarlo por tí mismo aunque tardes tiempo en descubrirlo. Sólo de esta manera no se te olvidará e irá desarrollandose la parte matemática de tu cerebro. Cuando creas que has dado con la solución comprueba tu respuesta (está un poco más abajo para evitar tentaciones de mirar).
Para llegar a la solución de este problema has obtenido una serie de números ¡Lo has conseguido! ¡Estos números forman la famosa SECUENCIA DE FIBONACCI, una sucesión infinita de números enteros cuyos primeros dos elementos son 0 y 1 y todos los elementos posteriores son la suma de los dos anteriores:
3-.
Ahora has llegado al periodo de observación. Busca los números de Fibonacci en la naturaleza. Pista: Busca por internet fotos de plantas, árboles, flores... o mejor aún, sal a buscarlas al campo. Coge una piña y mírala por el lado por donde estaba sujeta al árbol y observarás dos conjuntos de espiras: unas giran en el sentido de las agujas del reloj y otras en sentido contrario. Cuéntalas. Observa también las espiras de un girasol o una margarita. Observa tu cuerpo, tu brazo, tu mano, tus dedos... No tengas prisa. Descarta la posibilidad de leer toda la información al respecto por internet. ¡Tomate tu tiempo y disfruta de la búsqueda. ¡Descubrir tú mismo la relación con la secuencia de Fibonacci te dará más satisfacción!
Ahora con tiempo y calma coje la calculadora y caliéntate ese coco tan maravilloso que tienes e intenta ver relaciones entre los números de la secuencia. Hay un montón. Y en una de ellas encontrarás la proporción aurea que te llevará al número que buscamos...PHI φ (Solución más abajo)
Una vez creas tenerlo mira este vídeo y descubre el número phi y la magia de su pertenencia a la naturaleza:
-Si sumas los cuatro primeros términos y añades 1, te sale el sexto 1+1+2+3 + 1 = 8. Si sumas los cinco primeros términos y añades 1, te sale el séptimo 1+1+2+3+5 + 1 = 13.
-Si sumas los tres primeros términos que ocupan posición impar obtienes el sexto término 1+2+5 = 8. Si sumas los cuatro primeros términos que ocupan posición impar obtendrás el octavo término 1+2+5+13 = 21.
-Si sumas los tres primeros términos que ocupan posición par y añades 1 te dará el séptimo término 1+3+8 + 1 =1. Si sumas los cuatro primeros términos que ocupan posición par y añades 1, sale el noveno término 1+3+8+21 + 1 =34.
-Tomemos dos términos consecutivos, por ejemplo 3 y 5. La suma de sus cuadrados dará lugar al noveno(4+5) término de la sucesión: 9+25=34 .
Ahora probemos con 8 y 13: 64 + 169 = 233 que es el (6+7) decimotercer término de la sucesión.
-Si elevamos al cuadrado los cinco primeros términos y los sumamos, sale el producto del quinto y el sexto término: 12 + 12 + 22+ 32 + 52 = 40 = 5*8. Si hacemos lo mismo para los seis primeros términos, sale el producto del sexto y el séptimo término: 12 + 12 + 22+ 32 + 52 + 82 = 8*13.
-Si dividimos dos términos consecutivos de la sucesión, siempre el mayor entre el menor veamos lo que obtenemos:
Al tomar más términos de la sucesión y hacer su cociente nos acercamos al NÚMERO DE ORO:
Al tomar más términos de la sucesión y hacer su cociente nos acercamos al NÚMERO DE ORO:
4.- Ahora piensa dos números y construye empezando con ellos una sucesión como la de Fibonacci, es decir, en la que cada término sea la suma de los dos anteriores.
La suma de los 10 primeros términos de la sucesión será 11 veces el séptimo término. Esto sucede en la sucesión de Fibonacci y en cualquiera que se construya de la misma manera.
¿Te parece sorprendente? Construye varias sucesiones distintas que se cumplan como la de Fibonacci y comprueba que esto siempre sucede.
5.-Ahora intenta descubrir una ecuación partiendo de lo que te he dicho que dijo Euclides:
 |
| ¡La relación entre las dos partes en que dividimos el segmento es el número de oro phi! |
Y si ya entiendes de límites 
observa que cuanto mayores son los términos, los cocientes se acercan más a phi = 1,61803.... En lenguaje matemático:
"Si el lado del cuadrado vale 2 unidades podemos deducir que el lado mayor del rectángulo vale el doble de phi por lo que la proporción entre los dos lados es phi"
observa que cuanto mayores son los términos, los cocientes se acercan más a phi = 1,61803.... En lenguaje matemático:
6-. Encuéntralo en figuras geométricas:
RECTÁNGULOS ÁUREOS
1-Ahora observa estos rectángulos. Son áureos. Adivina por qué. De nuevo busca la relación con la Secuencia de Fibonacci y el número áureo.
2- Traza un rectángulo cuyos lados midan dos número consecutivos de la serie de Fibonacci. Haciendo un doblete desde el extremo superior izquierdo intenta obtener el cuadrado más grande posible. Lo recortamos y obtendremos otro rectángulo? ¿Qué aprecias? ¿Es parecido al rectángulo inicial?
Ahora haz lo mismo pero con un rectángulo cualquiera, por ejemplo, cuyos lados sean 6 y 10. ¿Qué observas? ¿Se asemeja al rectángulo inicial?
¿Tendrá que ver esto con la proporción áurea de Euclides?
Calcula el área del rectángulo y el área del cuadrado. ¿Son iguales las áreas? ¿Qué está sucediendo? ¿Es correcto el resultado que te ha salido? ¿Tendrá algo que ver con que 8, 13 y 21 sean números consecutivos de la sucesión de Fibonacci?
Pues bien, habrás llegado a la conclusión de que en el primer caso, al contrario que en el segundo caso, los rectángulos son semejantes y esto sucede porque es un rectángulo cuyos lados tienen la divina proporción que observó Euclides. Por tanto estamos ante rectángulos áureos.
Si recordamos la ecuación que hemos obtenido antes...
...podemos observar lo siguiente:
"Si el lado del cuadrado vale 2 unidades podemos deducir que el lado mayor del rectángulo vale el doble de phi por lo que la proporción entre los dos lados es phi"
3-¿Serías capaz de construir un rectángulo áureo a partir de dos rectángulos áureos? ¿y a partir de un cuadrado? ¡La solución salta a la vista!
4- Observa bien el dibujo ¿Se te ocurre alguna forma de saber si un triángulo es áureo?
Si se colocan dos rectángulos iguales como indica la figura al trazar una diagonal AB, observamos que pasa por el vértice C. Esta es una característica que sólo tienen los rectángulos áureos.
5- Ahora construyamos una serie de rectángulos utilizando los números de la sucesión de Fibonacci:
Coje una hoja de cuadros y dibuja un cuadrado de lado 1 (un cuadrado)y otro igual sobre él. Así obtenemos un primer rectángulo Fibonacci de dimensiones 2 x1.
Sobre el lado de dos unidades construye un cuadrado y obtendrás un nuevo rectángulo de 3x2.
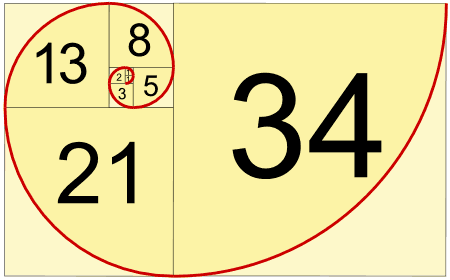
Sobre el lado mayor construimos otro cuadrado obteniendo así un rectángulo 5x3. Y así sucesivamente: 5x8, 8x13, 13x21...34x55, 55x89...
Fíjate que cada vez nos aproximamos más al rectángulo áureo.
Ahora une los vértices de estos rectángulos. Estás formando la espiral de Durero.
Hora de buscar!! Búscala en la naturaleza y en pinturas y construcciones hechas por el hombre...
Fibonacci, sin querer había encontrado la clave del crecimiento en la naturaleza:
En las conchas de los moluscos, en los cuernos de los rumiantes, las galaxias, tornados, agujeros negros, vuelo del águila cuando va a por su presa, en el cuerpo humano...
 |
| Partenón |
LA ESTRELLA PENTAGONAL
La estrella pentagonal o pentágono estrellado era, según la tradición, el símbolo de los seguidores de Pitágoras. Los pitagóricos pensaban que el mundo estaba configurado según un orden numérico, donde sólo tenían cabida los números fraccionarios. La casualidad hizo que en su propio símbolo se encontrara un número raro: el numero de oro.
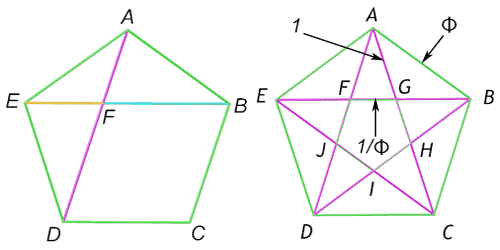
Dibuja un pentágono dentro de un círculo. Une 3 de los 5 puntos y luego traza una línea que una los otros dos puntos. Ahora ponte a medir y busca la proporción áurea al igual que hiciste con el rectángulo.
 |
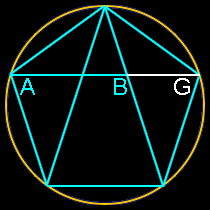Los segmentos AB, BG y AG están en proporción áurea
La relación entre la diagonal del pentágono y su lado es el número de oro
 |
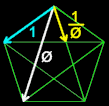
Dibuja tres líneas iguales y deja caer unas sobre otras como en la figura. Si se tocan justo en la mitad, ¿Tendrá que ver esto algo con la divina proporción?
 |
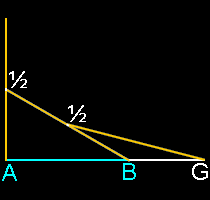| La proporción de AG y AB es Phi |
La proporción de AG con AB es Phi
Ahora inserta un cuadrado en un semi-círculo y observa. Busca la proporción áurea.
La proporción de AG con AB es Phi
Además de éstas hay un montón de construcciones geométricas que utilizándo el círculo producen proporciones áureas. Todo esto y mucho más en esta interesantísima página web dedicada al número de oro : Golden number .
También encontramos la divina proporción en las pirámides de Egipto. El triángulo rectángulo que lo contiene es de 51.83º , el coseno del cual es 0.618, es decir, Phi
Y por último propongo un juego, que no podría ser otro que el de las TARJETAS DE FIBONACCI
Nuestro objetivo es seguir ampliando y perfeccionando este tema y que éste nos lleve a otros como el tríángulo de Pascal. Pero lo iremos haciendo poco a poco. ESTO QUIERE DECIR QUE...
COTINUARÁ...
Y por último propongo un juego, que no podría ser otro que el de las TARJETAS DE FIBONACCI
 |
| ¡Esto lo has de recordar siempre!
|
¡Un avance!:
